Training a machine learning algorithm requires carefully selecting hyper-parameters. But with neural networks, this can easily go out of control with so many things to tune. Besides, the optimal values of these parameters vary from one dataset to another.
Leslie N. Smith in his paper – A Disciplined Approach to Neural Network Hyper-Parameters: Part 1 – Learning Rate, Batch Size, Momentum, and Weight Decay discusses several efficient ways to set the hyper-parameters in a neural network aimed at reducing training time and improving performance. In this blog post, I summarize the various strategies recommended in the paper. All the experiment figures have been directly taken from the paper.
Validation Loss Is Important
Validation/Test (have been used interchangeably) loss is very important to identify clues for overfitting and underfitting. The author suggests that identifying these clues early during training can allow us to tune the hyper-parameters with only a few epochs. This helps in avoiding complete grid or random searches.

For example, the above figure shows plots of the training loss, test loss and test accuracy for a learning rate range test (discussed later) of a residual network on the Cifar dataset to find suitable values of learning rate for training. We can see that in the learning rate range of 0.01-0.04, the test loss within the black box indicates overfitting (test loss is increasing). This information is not present in the other two curves. Now we know that this architecture has the capacity to overfit and a small learning rate will cause overfitting.
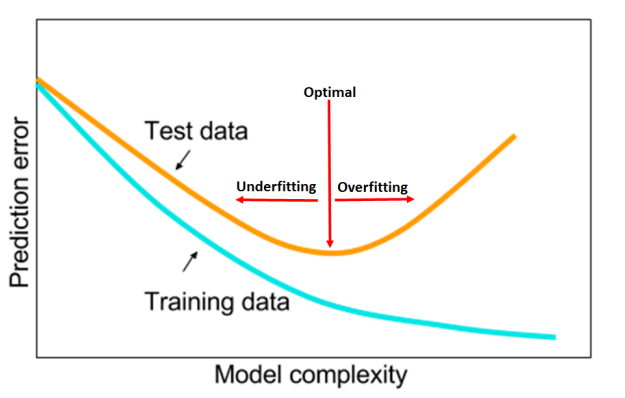
The key takeaway from this section is that achieving the horizontal part of the test loss is the goal of hyperparameter tuning. The test loss can be used to find the optimal hyper-parameters without performing a full training. If the hyper-parameters are set well at the beginning they will perform well through the entire training process.
Next, I will summarize the various tips and strategies provided by the author to identify the optimal values of – learning rate, batch size, momentum, and weight decay.
Learning rate
Learning rate is perhaps the most important hyper-parameter in neural network training. If the learning rate is too small, overfitting can occur. Large learning rates regularize the training but a very high value can cause the training to diverge. The key takeaways from this section would be –
- Using a large learning rate can lead to superconvergence.
- Use a Learning rate range test to find a large learning rate.
- 1cycle policy should be used with the LR range test.
- The total amount of regularization must be balanced.
Let’s discuss each of the above in detail.
Learning Rate Range Test
Instead of using a single value for the learning rate, the author proposes the use of learning rate range test. In this method, training is started from a very low value and is slowly increased to a large value until the loss starts to diverge. Test loss vs. learning rate is plotted and a value before the minimum test loss (where the loss still improves) is selected as the maximum value. The minimum value is ten times lower.
1cycle Policy
The author advises the use of 1cylce policy to vary the learning rate between this range. He recommends to do a cycle with two steps of equal lengths, one going from a lower learning rate to a higher one then going back to the minimum. The length of this cycle should be slightly less than the total number of epochs, and, in the last part of training, the learning rate is decreased more than the minimum, by several orders of magnitude.
Both these techniques were also introduced by Leslie in his paper – Cyclical Learning Rates for Training Neural Networks. For a detailed explanation of the 1cycle policy and the LR range test, check this awesome article by Sylvian Gugger – The 1cycle policy
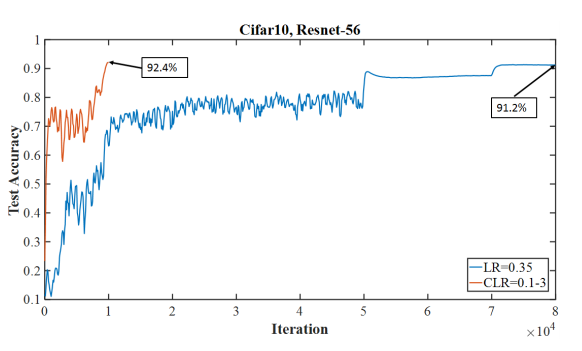
Superconvergence is a phenomenon where neural networks can be trained an order of magnitude faster than with standard training methods. The above figure is an example of superconvergence where training was completed in 10000 iterations with a 1cycle learning rate policy where learning rate went up to 3.0 instead of needing 80000 iterations with a fixed learning rate of 0.1.
Balance The Amount of Regularization
The author suggests that the amount of regularization must be balanced for each dataset and architecture. If we are using large learning rates (which have a significant underfitting effect), we must reduce other forms of regularizations.

The above figure shows that higher weight decay values do not go well with a higher learning rate (i.e. up to 3). Since a higher weight decay value provides a greater regularization effect, a balance in the amount of regularization is disturbed when used with a large learning rate which also has a regularization effect.
Batch Size
The batch size can also affect the underfitting and overfitting balance. Smaller batch sizes provide a regularization effect. But the author recommends the use of larger batch sizes when using the 1cycle policy.
Instead of comparing different batch sizes on a fixed number of iterations or a fixed number of epochs, he suggests the comparison should be done with a constant execution time. Since our goal is to maximize performance while minimizing the computational execution time.
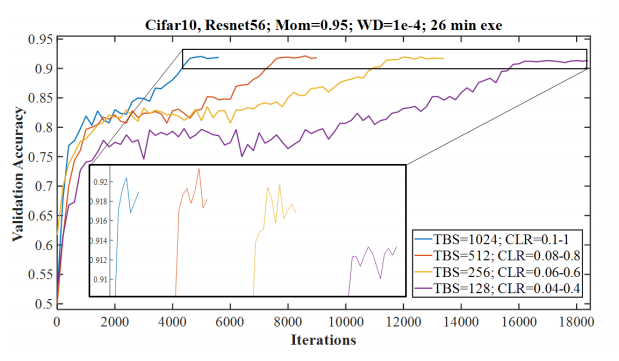
The above figure shows the validation accuracy for four different batch sizes. All the runs had the same execution time. We can see that larger learning rates were possible with higher batch sizes. The small black box gives a magnified view to highlight the difference in the accuracies. The results imply that it is beneficial to use large batch sizes. An important note – It was also found that unlike the final accuracy values the final loss values were lower for smaller batch sizes. Despite this, the paper recommends the use of a batch size that fits in our hardware’s memory and enable using larger learning rates.
Momentum
Momentum and learning rate are closely related. The optimal values of these hyper-parameters are interdependent. Momentum is designed to accelerate network training and has a similar impact on the weight updates as the learning rate. Like learning rates, it is valuable to set momentum as large as possible without causing instabilities during training.
Experiments show that unlike the learning rate range test, a momentum range test is not useful for finding an optimal momentum. The author recommends that short runs of 0.99, 0.97, 0.95, and 0.9 will quickly show the best value for momentum.
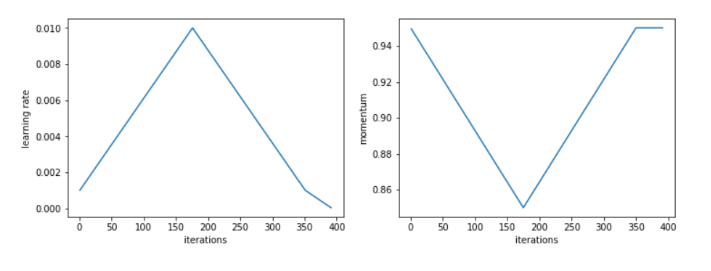
Source – https://sgugger.github.io/the-1cycle-policy.html
With cyclic learning rates, it is better to use a cyclical momentum that starts at the maximum momentum (one of the above values) and keeps decreasing to a value of 0.8 or 0.85 as the learning rate increases. The intuition behind this is that in this part of the training we would want to quickly go in new directions to find flatter areas, so the new gradients need to be given more weight. The momentum is then increased to the maximum value as the learning rate decreases in the second half of the 1cycle.
If a constant learning rate is used, then a large constant momentum (0.9 – 0.99) will help in speeding up the training. According to the author, the exact best value of momentum chosen during the whole training can give us the same final results, but using cyclical momentums helps us avoid multiple values running a number of cycles.
Weight Decay
Weight decay is a type of regularization method and is a key component during training. We have already discussed that we must balance the total amount of regularization during training. Hence, we need to set the values for weight decay properly.
The key takeaways from this section of the paper are –
- Cyclic weight decay is not helpful. Experiments show that weight decay is not like learning rates or momentum and the best value should remain constant throughout the training.
- A grid search is worthwhile and any difference due to the weight decay value is visible early in the training.
- If we have no idea of a reasonable value for weight decay, we should test 10-3, 10-4, 10-5, and 0.
- Smaller datasets and architectures seem to require larger values for weight decay while larger datasets and deeper architectures seem to require smaller values.
- The optimal weight decay is different if we search with a constant learning rate versus using a learning rate range test.
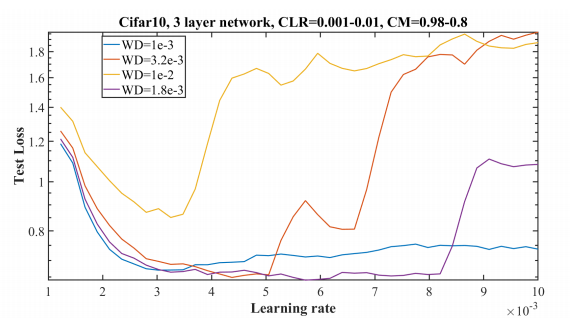
In the above experiment, a learning rate range test (LR=0.001 – 0.01) along with decreasing momentum (= 0.98 – 0.8) has been done with different weight decay values. It shows that a weight decay value of 1.8 x 10-3 is best as it remains stable for larger learning rates and also attains a lower validations loss.
Conclusion
The paper deals with perhaps the most common problem deep learning practitioners have – hyper-parameter tuning. I believe this is a must-read paper. I hope you enjoyed reading my post and now it would be easier if you go through the original paper. Thanks a lot. 🙂

it was such an helpful article for me. i would remain thankful if you update more articles on this topic regularly so that i can acquire more knowledge.
thank you .
LikeLike
Thanks a lot 🙂
LikeLike